[준비]A형 역량테스트 준비
https://blog.encrypted.gg/772
백준 강의내역 && barking dog 강의내역
자주하는 실수(B_D)
- 테스트에서는 pair, tuple 등은 인자로 넘기기보다는 전역으로 설정하는게 속편함
- 메모리초과 = 코딩실수, 불필요한 저장, 중복된 저장
- 인자로 사용하고 싶으면 따로
참조자에 대해 공부할 것.
메모리구조
- code는 어셈블리 영역
- stack 메모리에 지역변수와 함수의 인자가 올라감
- heap 메모리에 동적할당 변수가 올라감
- BSS에 초기화 전 전역변수가 올라감
- Data에 초기화 후 전역변수가 올라감
위의 총 5개의 메모리의 총합이 메모리사용량
stack 메모리는 1MB로 제한되는 경우가 있어 20,000~40,000 이상의 DEPTH를 가지면 터진다. 결론적으로 전역변수를 사용하는 경우가 꽤 많음
시간복잡도
- 시간복잡도 계산방법 - 코드를 보지않고 미리 계산! (코드를 먼저 짤 경우 시간이 오래걸린다.)
- 대략 1억 = 1초라고 생각하면 된다.
-
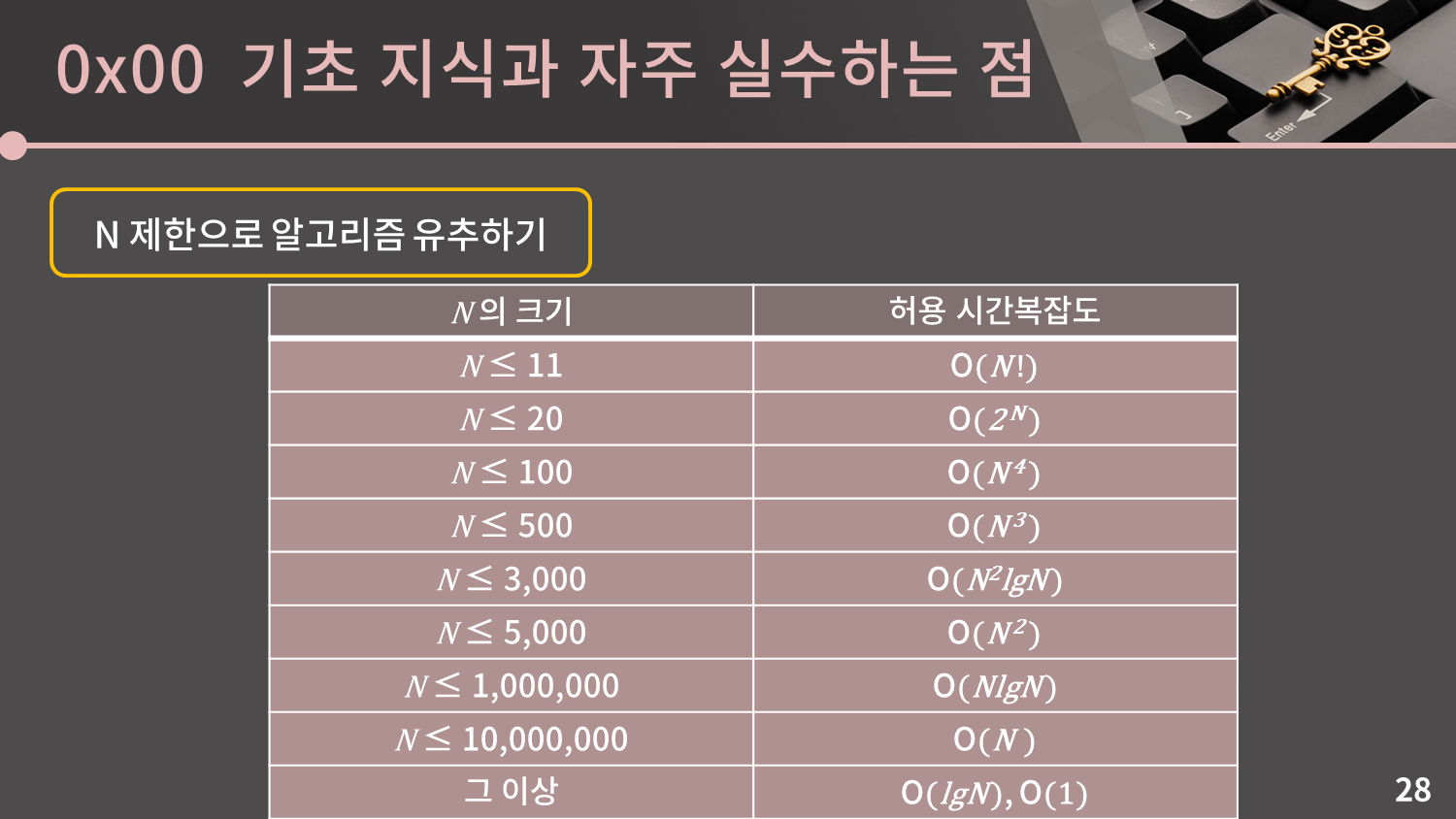
N을 미리알면 시간복잡도도 어느정도 예상가능 (EX: N= 1,000,000인 경우 N^2은 100억이니 절대안됨.)
- N=10,000이라도 가벼운연산의 경우 O(N^2)통과가능
- N=500,000이라도 무거운 연산 O(NlogN) 실패가능
- 맹신 X
TIP
- 디버깅보다는 출력을 이용하자
- STL오류 발생 시
무시후스택프레임을 보면된다. - 배열크기를 적절히 잡았는지 확인
- int 범위를 확인
- sort조건을 확인
- for문 범위를 확인
- 최소, 최대를 확인
OX퀴즈 (EZ, 8958)
자꾸 string to char배열을 검색하게 되어서 저장용으로 적어놓는 문제
string s;
char ox[80];
getline(cin, s);
strcpy(ox,s.c_str());
코딩팁
#include <functional>
//입출력 속도
ios::sync_with_stdio(0);
cin.tie(0);
//역소팅
sort(afterSort.begin(), afterSort.end(), greater<int>());
C++ 버전
- C++11부터 VLA(Variable Length Array) 지원
int arr[n] = {1,2,3};
- C++11부터 tuple, tie 사용가능
문제별 회고
양념 반 후라이드 반(16917, 브루트포스)
- 쉬운 문제인데 어렵게 생각해서 오래걸렸다.
- 문제를 꼼꼼히 읽을 것
BFS는 꽤 익숙하게 풀 수 있으므로 DFS 위주로 복습하자
움직이는 미로 탈출(16954, BFS)
- 벽은 1초에 한 칸씩 아래로 내려온다. (까다로운 조건)
- 크기 8X8 체스판에서 가장 왼쪽 아래칸에서 가장 오른쪽 위칸으로 이동 가능한지?
- 벽의 크기가 8X8이므로 8초동안의 벽을 모두 기록한다.
BFS에서는 할 수 있는게 같아야 같은 정점이다. (강의자료 택시, 버스 참고)
- 따라서 칸의 정보(r,c,t)로 시간에 대한 정보도 필요하다.
풀이(X)
-
- rock_count() 함수
- 예외처리를 위해 만든 함수로 설명 필요없음.
-
- move_wall 함수()
- bfs에서 이동하고 벽이 움직이기 때문에 만든 함수
-
- bfs()
- 상하좌우대각선 모두 이동이 가능하므로 매 실행마다 이동가능한 정점을 큐에 집어넣고 벽을 이동한 뒤 .. 실행
이거 실행되나?
어쩐지 실행이 안될것 같더라니 ㅎㅎㅎ 성공한 문제가 아니었다.
풀이(백준님 코드)
- tuple에 7,0,0을 입력한다. (시작점 가장왼쪽 아래 [7,0] & t=0)
- bfs를 실행한다.
- 상하좌우대각선 순차적으로 도는데
- nt= min(t+1, 8) 이니까 최대시간은 8초이다. (8초 후에는 내려갈 벽이 없으니까)
- isInside 조건을 확인하고
- if(a[nx-t][ny]==’#’) = t초 후에 내가 갈 곳이 벽이면 continue;
- if(a[nx-t-1][ny]==’#’) = t-1초 후에 내가 갈 곳이 벽이면 즉, 내가 이동하기 전에 벽이었으면 순서가 안맞으므로 못간다.
- 반복 이동조건: 내가 먼저 이동하고 벽이이동한다
#include <iostream>
#include <tuple>
#include <vector>
#include <string>
#include <queue>
using namespace std;
bool check[8][8][9];
int dx[] = {0,0,1,-1,1,-1,1,-1,0};
int dy[] = {1,-1,0,0,1,1,-1,-1,0};
int main() {
int n = 8;
vector<string> a(n);
for (int i=0; i<n; i++) {
cin >> a[i];
}
queue<tuple<int,int,int>> q;
check[7][0][0] = true;
q.push(make_tuple(7,0,0));
bool ans = false;
while (!q.empty()) {
int x, y, t;
tie(x,y,t) = q.front(); q.pop();
if (x == 0 && y == 0) ans = true;
for (int k=0; k<9; k++) {
int nx = x+dx[k];
int ny = y+dy[k];
int nt = min(t+1, 8);
if (0 <= nx && nx < n && 0 <= ny && ny < n) {
if (nx-t >= 0 && a[nx-t][ny] == '#') continue;
if (nx-t-1 >= 0 && a[nx-t-1][ny] == '#') continue;
if (check[nx][ny][nt] == false) {
check[nx][ny][nt] = true;
q.push(make_tuple(nx,ny,nt));
}
}
}
}
cout << (ans ? 1 : 0) << '\n';
return 0;
}
DFS와 BFS(1260, DFS, BFS)
- 좋은문제.
- 정점과 그래프형태로 나오므로 조~금 푸는게 다르지만
void dfs(int x){
cout << x+1 << " ";
if(check[x]) return;
check[x]=true;
for(int i=0; i<n; i++){
if(connection[x][i] && !check[i]){
dfs(i);
}
}
}
void bfs(int v){
queue<int> q;
q.push(v);
check[v] = true;
dist[v] = 0;
cout << v+1 << " ";
while(!q.empty()){
int x = q.front();
q.pop();
for(int y=0; y<n; y++){
if(!check[y] && connection[x][y]){
q.push(y);
check[y] = true;
dist[y] = dist[x]+1;
cout << y+1 << " ";
}
}
}
}
Two Dots(16929)
- Cycle에 관련된 문제이다.(그룹화에도 쓸 수 있을듯)
- 내 코드와 백준코드를 둘 다 보자.
백준코드
-
이전 칸과 다른 칸으로 연속해서 이동했을 때, 이미 방문한 칸을 방문했으면 사이클이 존재한다고 할 수 있다.
-
go() 함수
- (px,py) -> (x,y) -> (nx,ny)
- 인자 x,y = 시작점
- 인자 px, py = 이전점
- dfs이므로 왔던점이면 return
- 상하좌우를 살피며 isInside이고 px,py와 같지않다면
- 다음 함수로 진행해서 쭉쭉쭉 가다가 다음에 만나는 점의 color이 같다면 사이클존재 YES 출력
#include <iostream>
using namespace std;
char a[55][55];
bool check[55][55];
int n, m;
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
bool go(int x, int y, int px, int py, char color) {
if (check[x][y]) {
return true;
}
check[x][y] = true;
for (int k=0; k<4; k++) {
int nx = x+dx[k];
int ny = y+dy[k];
if (0 <= nx && nx < n && 0 <= ny && ny < m) {
if (!(nx == px && ny == py)) {
if (a[nx][ny] == color) {
if (go(nx, ny, x, y, color)) {
return true;
}
}
}
}
}
return false;
}
int main() {
cin >> n >> m;
for (int i=0; i<n; i++) {
cin >> a[i];
}
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (check[i][j]) continue;
bool ok = go(i, j, -1, -1, a[i][j]);
if (ok) {
cout << "Yes" << '\n';
return 0;
}
}
}
cout << "No" << '\n';
return 0;
}
내풀이
- dfs를 반복하면서
- 만약 depth가 4이상이고 다음 (x,y)가 이전x,y와 같다면 return true.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
int n, m, sx, sy;
bool check[51][51];
char map[51][51];
bool fin;
int dx[] = {0, 0, 1, -1 };
int dy[] = {1, -1, 0, 0 };
void dfs(int x, int y, char color, int count){
if(fin) return;
for(int i=0; i<4; i++){
int cx = x + dx[i];
int cy = y + dy[i];
if(cx>=0 && cx<n && cy>=0 && cy<m)
{
if(!check[cx][cy])
{
if(map[cx][cy] == color)
{
check[cx][cy] = true;
dfs(cx,cy, color, count+1);
}
}
else
{
if(count >=4 && sx == cx && sy ==cy)
{
fin = true;
return;
}
}
}
}
}
int main(){
cin >> n >> m;
//입력
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
char a;
cin >> a;
map[i][j] = a;
}
}
//dfs 실행
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
memset(check, false, sizeof(check));
sx = i; sy = j;
check[i][j]=true;
int cnt =1;
dfs(i,j, map[i][j], cnt);
if(fin)
{
cout<<"Yes"<<endl;
return 0;
}
}
}
cout << "No" << endl;
return 0;
}
미로탐색 (2178, BFS)
- 입출력 팁 2차원 배열 input이 공백없이 입력되는 경우
- 아래 코드처럼 입력받으면 된다.
int main(void) { cin >> n >> m; init(); //입력 for(int i1=0; i<n; i++){ for(int j=0; j<m; j++){ int temp; scanf("%1d", &temp); if(temp==1) map[i][j] = true; } } bfs(0,0); cout << check[n-1][m-1]; return 0; }
단지번호붙이기 (2667, BFS, 그룹화)
- 단지(연결된 집들의 모임)을 정의하고 단지에 번호를 붙인다.
불필요한 부분 제거코드
- 입력을 받고, 방문하지 않았던 단지에서 bfs를 반복한다.
- bfs는 일반적인 절차와 똑같이 진행하며
- isInside이고, 방문하지 않았으며 단지가 존재하는 위치이면
- 방문해서 groupCount만큼의 값을주어 map값을 변경한다.
void bfs(int sx, int sy) {
queue<pair<int, int>> q;
q.push(make_pair(sx, sy));
check[sx][sy] = 1;
while (!q.empty()) {
pair<int, int> x = q.front();
q.pop();
//동서남북
for (int i = 0; i < 4; i++) {
pair<int, int>y;
y = make_pair(x.first + dx[i], x.second + dy[i]);
int nx = y.first;
int ny = y.second;
if (isInside(nx, ny) && check[nx][ny] == 0 && map[nx][ny]>0) {
check[nx][ny] = check[x.first][x.second] + 1;
q.push(y);
map[nx][ny] = INF - groupCount;
group[groupCount]++;
}
}
}
groupCount++;
}
int main(void) {
cin >> n;
init();
//입력
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
int temp;
scanf("%1d", &temp);
if (temp == 1) map[i][j] = true;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(map[i][j]==1) bfs(i, j);
}
}
cout << groupCount << endl;
for (int i = 0; i < groupCount; i++) {
gc.push_back(group[i]);
}
sort(gc.begin(), gc.end());
for (int i = 0; i < gc.size(); i++) {
cout << gc[i]+1 << endl;
}
return 0;
}
모양만들기(16932, BFS, 그룹화)
- 단지번호붙이기의 심화판
-
백준코드와 내 코드를 모두 비교
- 하나를 변경할 수 있는게 문제다.
- 0을 1로 바꿀 수 있는 경우를 고려해서
- bfs로 미리 그룹사이즈를 구해놓고
- 계산한다
백준코드
#include <iostream>
#include <tuple>
#include <queue>
#include <algorithm>
using namespace std;
int n, m;
int a[1000][1000];
int group[1000][1000];
int group_size[1000*1000];
int groupn = 0;
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
void bfs(int sx, int sy) {
groupn += 1;
queue<pair<int,int>> q;
q.push(make_pair(sx,sy));
group[sx][sy] = groupn;
int cnt = 1;
while (!q.empty()) {
int x, y;
tie(x,y) = q.front(); q.pop();
for (int k=0; k<4; k++) {
int nx = x+dx[k];
int ny = y+dy[k];
if (0 <= nx && nx < n && 0 <= ny && ny < m) {
if (group[nx][ny] == 0 && a[nx][ny] == 1) {
group[nx][ny] = groupn;
q.push(make_pair(nx,ny));
cnt += 1;
}
}
}
}
group_size[groupn] = cnt;
}
int main() {
cin >> n >> m;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
cin >> a[i][j];
}
}
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (a[i][j] == 1 && group[i][j] == 0) {
bfs(i, j);
}
}
}
int ans = 0;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (a[i][j] == 0) {
vector<int> near;
for (int k=0; k<4; k++) {
int nx = i+dx[k];
int ny = j+dy[k];
if (0 <= nx && nx < n && 0 <= ny && ny < m) {
if (a[nx][ny] == 1) {
near.push_back(group[nx][ny]);
}
}
}
sort(near.begin(), near.end());
near.erase(unique(near.begin(), near.end()), near.end());
int sum = 1;
for (int neighbor : near) {
sum += group_size[neighbor];
}
if (ans < sum) ans = sum;
}
}
}
cout << ans << '\n';
return 0;
}
내 소스
#include <iostream>
#include <math.h>
#include <queue>
#include <vector>
#include <algorithm>
#define INF 987654321
using namespace std;
int n,m, groupCount,maxGroupSize=0;
int map[1000][1000], check[1000][1000];
//사이즈 늘어날 수 있음
int group[1000000];
vector<int> groupV;
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
bool isInside(int x, int y){
if(x>=0 && x<n && y>=0 && y<m) return true;
else return false;
}
bool findDuplGroup(int idx){
int temp = groupV.size();
for(int i=0; i<temp; i++){
//이미 확인했던 그룹이면
if(groupV[i]==idx) return false;
}
return true;
}
void pickZero(int sx, int sy){
int temp=0;
for(int i=0; i<4; i++){
int nx = sx + dx[i];
int ny = sy + dy[i];
//8.격자안에 위치하고 그룹에 속한경우
if(isInside(nx,ny) && map[nx][ny]>1){
//상 하 좌 우에 이미 합친 Group이 없는 경우....
if(findDuplGroup(INF-map[nx][ny])){
groupV.push_back(INF-map[nx][ny]);
//group[INF-map[nx][ny]] = 인접한 그룹의 사이즈 + 1, groupcount가 1이 적게 들어가있어서그렇다
temp += group[INF-map[nx][ny]]+1;
}
}
maxGroupSize = max(maxGroupSize, temp);
}
groupV.clear();
}
void bfs(int sx, int sy){
queue<pair<int,int>> q;
q.push(make_pair(sx,sy));
check[sx][sy] = 1;
map[sx][sy] = INF-groupCount;
while(!q.empty()){
pair<int, int> x = q.front();
q.pop();
//동서남북
for(int i=0; i<4; i++){
pair<int,int>y;
y = make_pair(x.first+dx[i], x.second+dy[i]);
int nx = y.first;
int ny = y.second;
//2.격자안에 있고, 아직 방문한적이 없으며, 집이 있는 경우
if(isInside(nx, ny) && check[nx][ny]==0 && map[nx][ny]>0)
{
//3.몇 번째로 방문했는지 표시하고
check[nx][ny] = check[sx][sy]+1;
//4.큐에 넣어 다음 search 준비를 하고
q.push(y);
//6.map값도 변경
map[nx][ny] = INF-groupCount;
//5.group화를 위해 groupCount를 세준다.
group[groupCount]++;
}
}
}
}
int main(void) {
cin >> n >> m;
init();
//입력
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
int temp;
scanf("%1d", &temp);
if(temp==1) map[i][j] = true;
}
}
groupCount=0;
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
if(map[i][j]==1)
{
//1. 처음 등장한 1에서 BFS()
bfs(i,j);
groupCount++;
}
}
}
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
if(map[i][j]==0)
{
//7. 0인 녀석들을 골라 1로 변경
pickZero(i,j);
}
}
}
//+1인 이유는 위에서 자기자신을 계산하지 않았기 때문이다.
cout << maxGroupSize+1;
}
댓글남기기